Analyse des rôles sémiotiques de quelques flèches dans des manuels de physique.
Alaric Kohler
&
Bernard Chabloz
Haute École Pédagogique BEJUNE
Pour citer ce document
télécharger le pdfIntroduction
Les schémas et esquisses constituent des objets sémiotiques complexes, jouant un rôle important pour l’activité de modélisation. De manière à aborder progressivement cette complexité, nous proposons ici dans un premier temps de nous intéresser à un objet sémiotique précis: la flèche.
Le dessin de flèches est une pratique commune en classe de physique. Les manuels et autres feuilles d’exercices à destination des élèves en font également un usage courant, en particulier sur des schémas ou esquisses qui accompagnent le texte rédigé. Néanmoins, le fait qu’il s’agisse d’une pratique courante n’en fait pas une pratique banale pour autant, et surtout ne conduit pas forcément à des usages conventionnels, réguliers ou rigoureux.
Pour mener l’enquête, nous nous intéresserons aux rapports entre les caractéristiques des objets sémiotiques eux-mêmes (sens et direction de la flèche, rendu du tracé, couleurs, etc.) et les rôles que ces objets jouent sur les schémas ou esquisses où ils ont été dessinés.
Premièrement, l’objet sémiotique flèche ne remplit pas toujours le même rôle dans la construction de sens, qu’elle soit communication ou interprétation. Nous analyserons donc le rôle sémiotique (Kohler, 2014) des diverses flèches rencontrées dans les schémas et esquisses étudiées ci-dessous. Nous montrerons que des flèches identiques sont parfois utilisées pour des rôles sémiotiques différents.
Il convient de ne pas confondre rôle sémiotique et la fonction sémiotique, telle qu’elle est définie chez Piaget et qui fait référence à la capacité de faire usage de signes, symboles et icônes en général. Le rôle sémiotique fait référence à un usage spécifique d’un signe, symbole ou icône dans un objectif de communication ou de construction de connaissance situé historiquement, socialement, éventuellement en référence à un système sémiotique comme la physique, etc.
Du point de vue de la communication, le fait qu’un objet sémiotique comme la flèche joue plusieurs rôles sémiotiques dans un manuel ou – comme nous le montrons ci-dessous – dans un même schéma, peut constituer une source de difficultés d’interprétation pour les apprenants. En effet, les élèves ou novices dans un domaine sont confrontés à la double tâche d’assimiler les objets sémiotiques eux-mêmes en tant qu’éléments d’un système sémiotique complexe – la discipline physique, – et de s’approprier ces mêmes objets pour en faire usage, de manière à les utiliser comme outils sémiotiques permettant de répondre à des questions, construire des modèles, étayer un discours, résoudre des problèmes, etc.
Deuxièmement, après avoir identifié quelques rôles sémiotiques en analysant les flèches, nous montrerons aussi dans les exemples ci-dessous que des objets sémiotiques différents sont parfois utilisés pour un même rôle sémiotique. Cet usage d’objets sémiotiques multiples pour un même rôle sémiotique peut également constituer un risque de malentendu, l’interprétation ne pouvant dès lors se reposer sur l’observation de régularité et d’une certaine consistance d’usage de ces objets sémiotiques pour en inférer le sens.
Première analyse
Un même objet sémiotique pour des rôles sémiotiques différents, et vice-versa.
Commençons par un exemple issu du manuel Tavernier (Pierrard, 2009, p.323)1, dont nous avons reproduit un schéma ci-dessous (figure 1). Ce schéma présente deux flèches dessinées de manière semblable, mais jouant deux rôles sémiotiques différents.
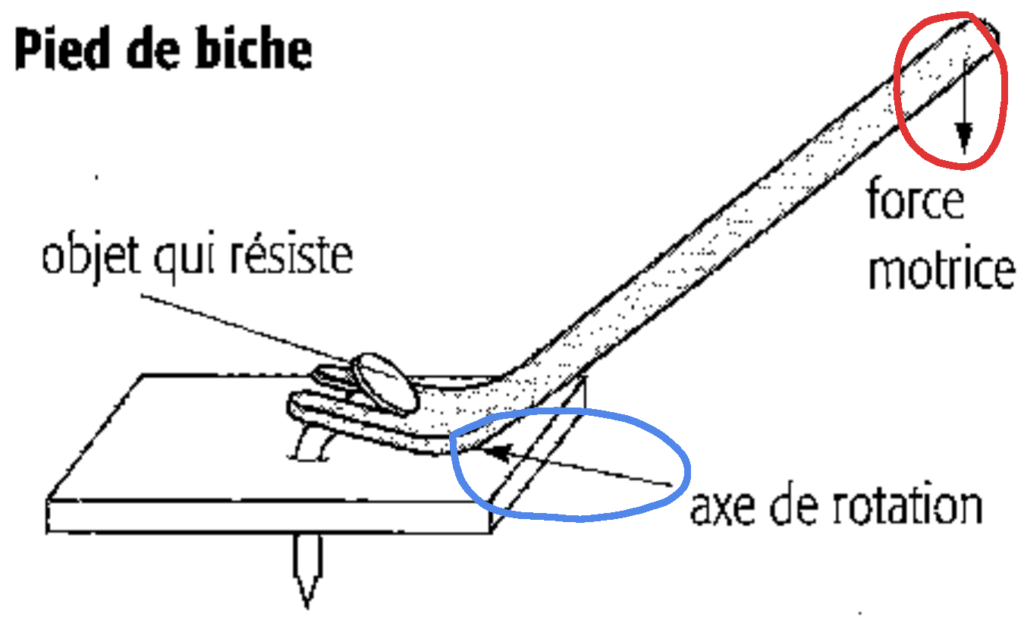
Figure 1. Exemple de “leviers simples”, extrait de Pierrard, 2009, p.323.
La première flèche que nous avons entourée en rouge, désigne l’application d’une force en faisant figurer son sens, sa direction et peut-être son intensité – quoique d’une manière non graduée. Une seconde flèche, que nous avons entourée d’un cercle bleu, désigne un endroit de l’esquisse de manière à l’associer à la légende “axe de rotation”.
Deux rôles sémiotiques différents peuvent être identifiés à partir de ces deux usages de l’objet sémiotique flèche.
1. La flèche entourée de rouge remplit un rôle de modélisation : l’objet dessiné (la flèche) reprend certaines caractéristiques de l’objet modélisé (l’application d’une force), à savoir la direction, le sens, l’intensité (peut-être) et le point d’application.
2. La flèche entourée de bleu remplit un rôle de pointage : elle se termine là où devrait se diriger l’attention du lecteur. En ce sens, elle constitue un déictique non verbal, au même titre que le mot ça ou ici, et a pour fonction de contribuer à construire une attention conjointe dans l’interaction sociale entre l’auteur du manuel et son lecteur.
Un autre phénomène intéressant est à relever sur l’esquisse ci-dessus : l’usage de deux objets sémiotiques différents dans le rôle du pointage. La flèche est utilisée pour pointer un lieu de l’esquisse relié à la légende “axe de rotation”, et un trait simple est utilisé dans le même rôle de pointage, relié à la légende “objet qui résiste”.
Modéliser l’application d’une force
Dans le schéma reproduit ci-dessus (cf. figure 1), nous avons vu que la flèche jouait un rôle de modélisation de l’application d’une force. En tant que telle, la flèche ne représente qu’un instantané de la dynamique du phénomène qu’elle modélise : un bref instant plus tard, elle aura peut-être une orientation ou une intensité différente. D’ailleurs, le propos de l’auteur n’est pas ici de suggérer une variation ou un mouvement, ce schéma modélise une situation statique ou quasi statique, quand bien même le novice peut interpréter le schéma comme désignant une rotation du pied-de-biche – la légende axe de rotation peut effectivement susciter ce malentendu. La convention qui dans notre culture associe un mouvement à l’objet flèche ne devrait donc pas être activée par le lecteur. Si elle l’est, l’amalgame classique entre force et vitesse peut s’en trouver renforcé (Viennot, 1979), d’autant plus que, précisément, il reste sensé dans les situations quasi statiques ou stationnaires, puisque force motrice et mouvement ont alors même direction et même sens2.
Dans un schéma modélisant une situation dynamique non stationnaire, on trouvera une même flèche pour représenter une force motrice qui cette fois-ci ne sera plus qu’exceptionnellement parallèle au mouvement : son caractère instantané devient alors essentiel à la compréhension de la description physique du phénomène ! Ainsi, l’usage d’objets sémiotiques statiques comme une flèche — par contraste avec un document vidéo par exemple — conduit bien à une modélisation du phénomène dynamique à un instant précis, mais cette réduction n’a pas la même portée selon le contexte. Or, il s’agit là souvent d’une décision — contrainte par les outils à disposition — qui reste implicite et peut également conduire les apprenants à des difficultés d’interprétation, notamment s’ils s’attendent à ce que la flèche représente l’ensemble du phénomène dynamique plutôt qu’un instantané de celui-ci, et plus encore si rien ne les rend attentifs à l’importance primordiale de cette instantanéité dans les situations non stationnaires.
Deuxième analyse
Représentation du mouvement et de la variabilité.
Dans d’autres cas, par exemple dans le schéma ci-dessous (figure 2), l’objet sémiotique flèche représente un mouvement.
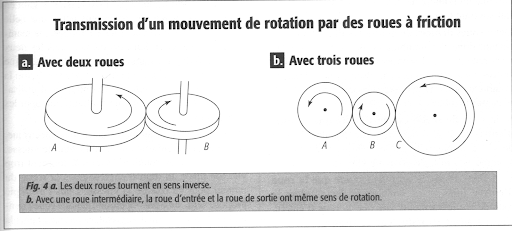
Figure 2. Transmission d’un mouvement, extrait de Pierrard, 2009, p.345.
Dans ce rôle sémiotique, la flèche est un signe qui s’adapte aux propriétés du support papier dans le but de représenter un objet en mouvement sans disposer d’un support lui-même en mouvement ou en transformation, comme ce serait le cas pour un document vidéo par exemple. Dans ce cas, le sens que prend la flèche peut être passablement différent selon qu’il s’agit de l’auteur du manuel, d’un enseignant de physique, ou d’un élève ou novice dans le domaine. Chez le novice, la flèche joue probablement le rôle d’une référence directe au mouvement, qui est évoqué. Avec un peu d’imagination, le lecteur novice voit la roue tourner sur la figure 2. Pour le spécialiste, par contre, la flèche fait plutôt référence à un vecteur, que l’on peut définir par trois caractéristiques : sens, orientation et intensité.
On remarquera que la longueur des flèches dessinées sur la figure 2 suggère des variations d’intensité selon le diamètre des roues. Pour ce qui est du sens et de la direction, les flèches dessinées permettent effectivement de comprendre le sens de la rotation, mais elles diffèrent d’un vecteur du fait qu’elles sont positionnées sur la roue et que leur tracé est courbe. Un vecteur ne peut être dessiné nulle part — n’ayant aucune position — et parler de la courbure de son intensité n’aurait aucun sens (à moins que la courbure de l’espace, justement… ?). Cette courbure a plutôt à voir avec la trajectoire. Or, mouvement et trajectoire sont clairement différenciés en physique, au moins depuis Newton, alors que le sens commun les confond volontiers. C’est selon Koyré (1968) ce qui permet à Newton une approche radicalement nouvelle, à savoir une modélisation mathématique du mouvement, qui rompt avec la physique médiévale visant la prédiction de trajectoires, et tout particulièrement celles des boulets de canon.
Les différences d’interprétation entre novice et expert mise en évidence pour l’usage de la flèche pour faire référence à un mouvement peuvent conduire à un malentendu bien spécifique : alors que pour l’expert il s’agit d’une modélisation d’un phénomène dynamique à un instant précis, le novice pour qui la flèche représente effectivement le mouvement, interprète la modélisation implicite au schéma qu’il lit comme une modélisation de l’ensemble du phénomène dynamique, plutôt qu’un instantané de celui-ci.
Or, la flèche n’est pas toujours utilisée pour modéliser des phénomènes dynamiques ou en mouvement — on vient de voir un contre-exemple à la figure 2. Elle n’est même pas toujours utilisée pour modéliser, puisque l’un de ses rôles sémiotiques courants est le pointage (voir p.ex. la flèche comme déictique à la figure 1).
Troisième analyse
De flèches différenciées dans un même rôle sémiotique de pointage
Dans l’extrait du manuel de Faucher (1961) présenté ci-dessous (voir figure 3, ci-dessous), le risque de malentendu que nous venons de décrire a été prévenu en choisissant d’inclure dans la représentation (le schéma) plusieurs instants – deux en l’occurrence, mais c’est bien la pluralité qui est significative ici. Cela se traduit sur le dessin par deux flèches différentes, l’une en traitillé faisant référence à un instant antérieur à l’accrochage d’un poids et l’autre en trait continu représentant l’inclinaison d’un support flexible dans sa position d’équilibre après l’accrochage d’un poids à son extrémité.
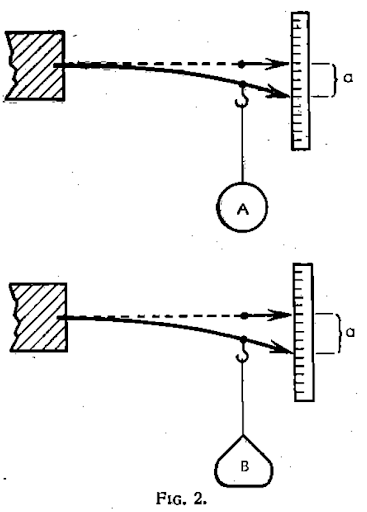
Figure 3. Illustration de “la mesure d’une force”, extrait de Faucher, 1961, p.17.
Dans ce schéma de la figure 3, les flèches ne représentent pas des vecteurs forces, mais plutôt l’action du physicien ou l’orientation de son regard lorsqu’il mesure la distance ( sur le schéma) entre les extrémités du support flexible sans poids — en position horizontale — et avec un poids suspendu — en position inclinée. Deux poids différents sont représentés sur le schéma, à nouveau pour évoquer la pluralité des inclinaisons possibles selon les poids accrochés (A ou B sur les schémas de la figure 3). Le choix d’une lettre (𝒂) pour faire référence à la distance mesurée indique aussi, selon un usage courant dans les manuels des années soixante, qu’il s’agit ici d’une variable.
La sémiotique du schéma reproduit par la figure 3 procède d’une réflexion sur la représentation d’un mouvement à l’aide de la représentation de deux instants différents, et sur la représentation de la variable (la distance de l’extrémité du support flexible par rapport à l’horizontale) à l’aide de la représentation de deux poids différents (A et B), auxquels une forme différente a été donnée pour suggérer une différence de masse. Si, au sens de la physique, il s’agit de mécanique statique, du point de vue de l’élève il s’agit effectivement de comprendre le mouvement du support flexible pour comprendre la mesure de la force que ce schéma illustre. Au niveau sémiotique cependant, ce n’est pas la flèche qui représente ce mouvement comme on aurait pu s’y attendre, mais le fait de mettre plusieurs (deux) traits pour représenter deux instants d’équilibre parmi une infinité. Cette analyse relève la pertinence du soin apporté à différencier ces deux traits par une ligne continue pour l’un et discontinue pour l’autre. Que représente alors la flèche dans ce schéma ?
La flèche dans ce schéma ne représente pas la force, mais est plutôt utilisée dans son rôle sémiotique de pointage : elle pointe sur l’endroit de l’outil gradué qu’il faut regarder pour prendre la mesure de la force. Si le schéma de la figure 3 a bonne une cohérence interne au niveau sémiotique, l’objet sémiotique flèche est néanmoins utilisé dans le même manuel, sur la page contiguë, dans un autre rôle sémiotique (cf. quatrième analyse). Cet exemple montre qu’au-delà de la question de la cohérence interne des rôles sémiotiques, c’est-à-dire les rôles des objets sur un même schéma, se pose la question de la cohérence externe des rôles sémiotiques jouée par l’objet flèche, par exemple au sein d’un manuel, d’une séquence d’enseignement ou, encore plus généralement, dans les sciences physiques.
Quatrième analyse
Des flèches pour désigner des forces
En mécanique, la flèche est souvent utilisée pour représenter un vecteur, qui est lui-même un modèle mathématique du concept de force (cf. figure 4, par exemple).

Figure 4. Illustration au début du chapitre des forces, extrait de Faucher, 1961, p.16.
Un schéma, dans le même manuel de Faucher (1961), présente l’objet sémiotique flèche dans un rôle de modélisation d’un vecteur représentant une force, et fait usage de deux types de flèches différents (cf. figure 5). Le schéma est produit au chapitre sur les couples et le moment de force.
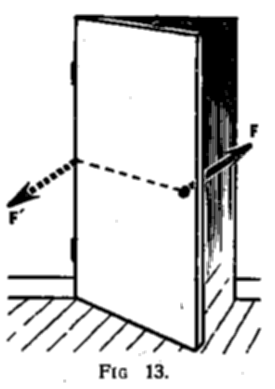
Figure 5. Illustration d’un couple, extrait de Faucher, 1961, p.49.
En comparant ce schéma à celui reproduit par la figure 1, il est possible de mettre en évidence de nouvelles questions portant précisément sur l’usage que font les manuels de physique de l’objet flèche. Nous étions précédemment sur des incohérences à l’intérieur d’un schéma, puis entre schémas au sein du même manuel. Les décalages ou absences de cohérence entre manuels différents nous permettent d’élargir la discussion sur un objet sémiotique comme la flèche. La comparaison de la figure 1 et de la figure 5 interpelle non seulement quant au rôle sémiotique de la flèche sur des schémas de physique — nous avons identifié un rôle de pointage et un rôle de modélisation d’un vecteur — mais aussi quant aux normes qui devraient être établies pour assurer une cohérence de l’outil.
Par exemple, dans la figure 5, la flèche jouant un rôle de modélisation d’un vecteur est appliquée sur un point précis d’une illustration faisant usage de perspective pour représenter un objet en trois dimensions. De plus, à la force désignée F correspond une force opposée F’ de manière cohérente avec la théorie newtonienne. Cependant, cette flèche n’est pas placée au même endroit, mais reliée à l’autre flèche par une ligne traitillée de manière à signifier qu’elles s’exercent sur le même objet et qu’elles sont “en contact” par l’intermédiaire d’un objet solide, la porte. Troisièmement, un trait discontinu est dessiné pour la flèche représentant F’ pour signifier qu’il s’agit d’une force d’un autre genre, une force de réaction. Cette force n’est en effet pas exercée par la personne qui ouvre la porte, il s’agit d’une force de réaction. Aucune de ces précautions n’a été prise dans le schéma de la figure 1.
Cinquième analyse
Des flèches diverses pour différencier des rôles sémiotiques (ambigus).
Dans le schéma reproduit par la figure 6, nous trouvons deux flèches différenciées par le trait continu ou discontinu et par le point d’origine de la flèche, tantôt au centre de l’objet et tantôt en surface.
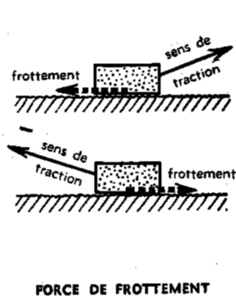
Figure 6. Illustration de forces de frottement, extrait de Faucher, 1961, p.27.
Dans l’usage qui est fait de ces deux types de flèche sur le schéma de la figure 6, les flèches jouent toutes un rôle de modélisation, mais les deux types de flèche ne modélisent pas le même objet, et sont utilisés en cohérence avec ce qu’elles représentent. Les flèches au trait discontinu modélisent des vecteurs, un objet théorique représentant à son tour des forces, alors que les flèches en trait continu désignent la force de traction exercée sur l’objet ou peut-être uniquement le sens du mouvement provoqué par la traction. Au sens de quoi se réfère le mot sens dans la légende “sens de la traction” ? Voilà un bel exemple d’ambiguïté, puisque, s’il s’agit d’une force, alors le sens du mouvement n’est donné (indirectement) que par composition du vecteur modélisant la force de traction avec le vecteur modélisant la force de frottement. Peu importe, me direz-vous, cela revient au même pour ce qui est du schéma de la figure 6. On retrouve néanmoins ici l’amalgame entre sens de la force et sens du mouvement, avec un schéma qui accrédite l’idée de l’état stationnaire : l’objet était immobile, puis on le tire en avant, et donc il avance et la force de frottement le freine3. La phase transitoire d’accélération est complètement éludée !
La différence entre les types de flèches est aussi faite à l’aide du point de départ de la flèche : la flèche dénotant un vecteur prend comme point de départ sur le schéma le centre de la zone de contact avec le sol, pour représenter le point d’application de la force de frottement, alors que la flèche désignant la force de traction (ou le sens du mouvement) est appliquée à la surface “avant” de l’objet, comme si elle représentait en même temps l’objet concret corde qui tire le wagonnet et la force ou le mouvement. Cette ambiguïté rejoint ici la polysémie de tirer ou attirer : en physique, attirer ne signifie pas faire venir.
Les flèches absentes sur le schéma jouent-elles un rôle dans l’interprétation ?
Une question se pose relativement aux flèches qui ne sont pas dessinées sur le schéma de la figure 6 : du moment qu’une force est représentée sur le schéma, ne devrait-on pas trouver toutes les forces qui s’appliquent sur l’objet représentées avec le même type de flèche ? À la défense du choix qui est fait ici dans le manuel de ne représenter que les forces de frottement, ce schéma se trouve dans une planche d’une page entière dont le but est d’illustrer les “principales catégories de forces” et chaque schéma de cette page n’en présente qu’une seule. Néanmoins, la question posée est liée aux difficultés d’interprétation soulevées ci-dessus : si toutes les forces s’appliquant sur le chariot à un moment spécifique (quand il est encore immobile, ou à la fin de son accélération, par exemple) étaient effectivement dessinées, cela permettrait au lecteur d’inférer que “sens de la traction” désigne effectivement le sens d’une force de traction. C’est dire que les flèches qui ne sont pas dessinées jouent aussi, au moins parfois, un rôle dans les interprétations des flèches effectivement dessinées.
Ceci n’a rien d’étonnant, l’interprétation reposant largement sur des processus d’inférence pour lesquels la cohérence et la répétition sont des critères importants. Si mon schéma comporte quatre flèches dont trois désignent sans ambiguïté des forces, l’ambiguïté de la désignation de la quatrième est résolue en faveur de la cohérence de l’ensemble : il s’agit aussi d’une force. Cet exemple met en évidence l’importance de la cohérence dans les usages des objets sémiotiques : quelles seraient les normes qui pourraient garantir cette cohérence sémiotique et soutenir le processus d’interprétation ?
Sixième analyse
Des flèches semblables pour représenter diverses grandeurs vectorielles.
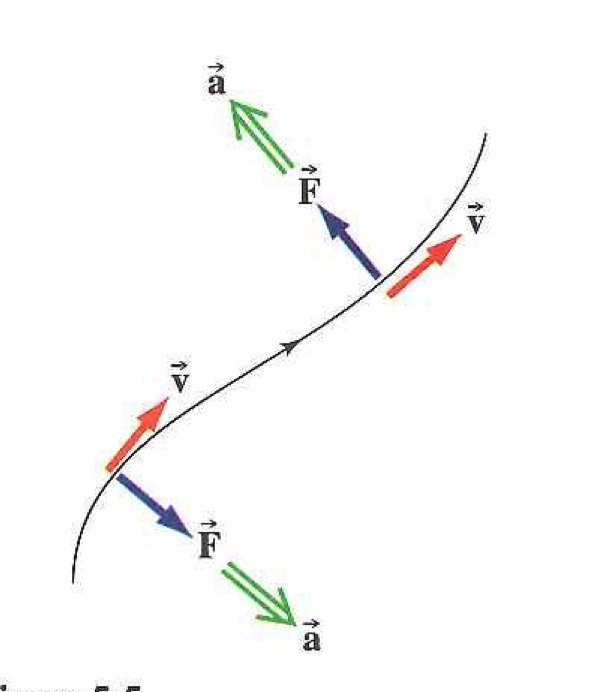
La représentation d’une trajectoire “munie” de vecteurs vitesse, accélération et force est un autre objet graphique classique comportant des flèches, auquel on réfère pour exposer, comprendre ou appliquer la 2e loi de Newton.
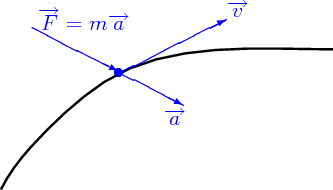
Figure 7. Illustration des grandeurs vectorielles qu’implique la 2e loi de Newton4
La figure 7 montre bien les trois vecteurs en question, cependant les flèches seules ne suffisent pas à suggérer la distinction, pourtant essentielle, que l’apprenant doit faire entre les types de grandeur physique. Une question comme « Pourquoi le vecteur vitesse est-il plus long que le vecteur accélération ? » révèle une probable absence de cette distinction, éventuellement corroborée par des manipulations graphiques dépourvues de sens en physique, comme l’addition ou la soustraction de tels vecteurs5.
Sur la figure 7, on a pris soin de placer une légende pour chacune de ces flèches, qui peuvent en suggérer le type de grandeur physique, à ceci près que l’habitude sémiotique de choisir l’initiale comme signifiant ( pour l’accélération, par exemple) ne favorise pas l’interprétation. En particulier, l’objet F ne représente pas (en général) une des forces subies par l’objet modélisé par la tache bleue, mais bien la résultante de toutes les forces qu’il subit. De plus, cette résultante des forces semble “pousser” l’objet, si on interprète ainsi le fait que la pointe de la flèche le touche. Traditionnellement, les vecteurs sont plutôt représentés par des flèches “issues” des objets qui ont ces caractéristiques (comme les vecteurs vitesse de l’objet et accélération de l’objet) ou qui subissent ces actions extérieures (les forces subies par l’objet) : c’est bien ainsi qu’il convient de lire la 2e loi de Newton.
Notons au passage que les relations des grandeurs physiques à l’objet précisées ci-dessus verbalement, ne sont signifiées d’aucune manière dans l’écriture mathématique de la 2e loi de Newton : seule une maîtrise des signifiés permet de lire cette loi à partir de son écriture dans le sens prévu en physique.
Septième analyse
Des flèches de couleur différentes pour représenter diverses grandeurs vectorielles.
Les auteurs de la figure 8, par contre, adoptent un code de couleur qui permet, même sans légende, de distinguer les types de grandeur physique.
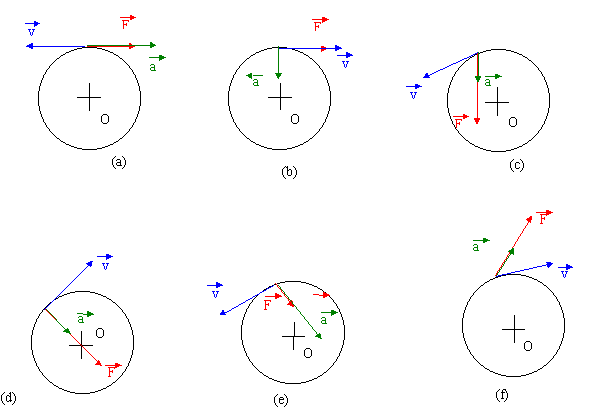
Figure 8. Exercice à propos des grandeurs vectorielles qu’implique la 2e loi de Newton6

Cet artifice offre à l’enseignant la possibilité de cette provocation : ceci n’est pas un triangle.
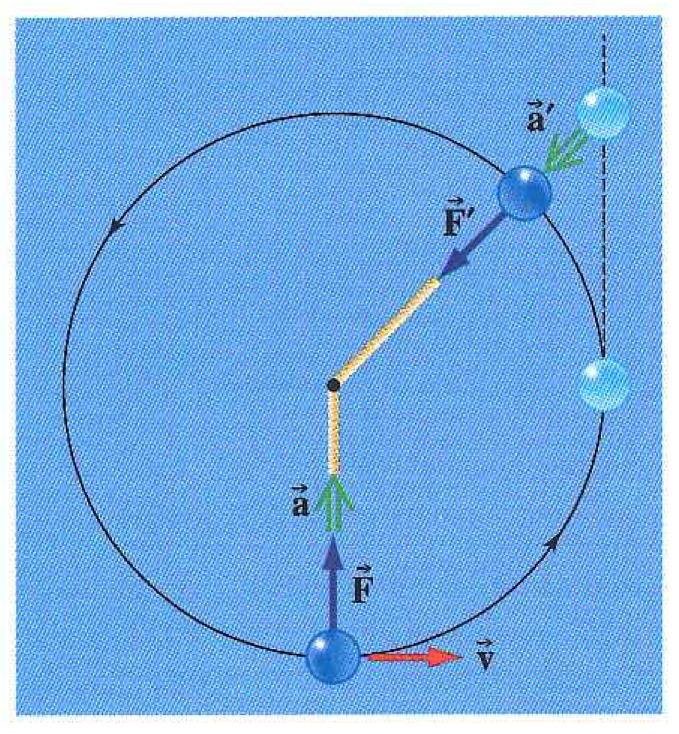
Les figures 9 et 10 montrent un autre exemple d’utilisation d’un tel code, avec en plus une forme de flèche particulière pour le vecteur accélération.
| Figure 9. Illustration des grandeurs vectorielles qu’implique la 2e loi de Newton, extrait de Benson, 1999, p.121. |
Figure 10. Idem dans le cas d’un mouvement circulaire, extrait de Benson, 1999, p.152. |
Même différenciation entre forces et vitesse dans la figure 10, avec toutefois une source potentielle de malentendus dans la mesure où les vecteurs obliques R1 et respectivement R2 ne sont pas de “nouvelles forces” subies par la voiture, mais bien les résultantes de forces horizontales (frottement et traction) et verticales (soutiens du sol) déjà présentes sur le schéma.
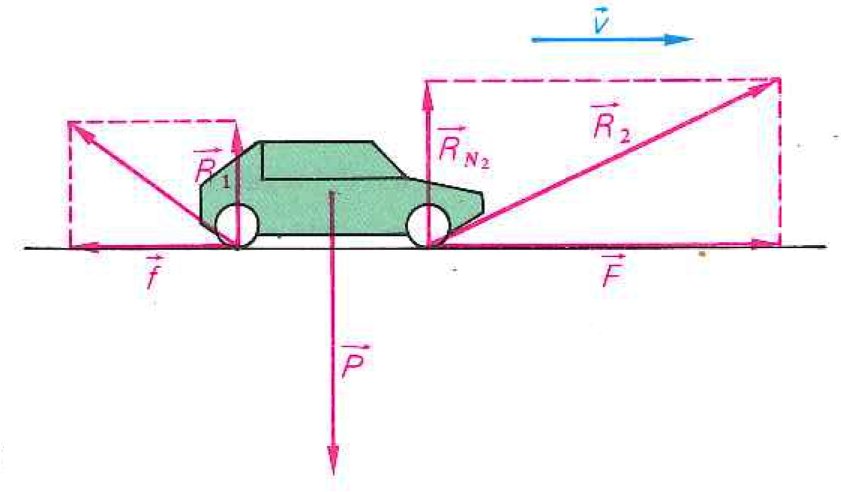
Figure 10. Forces subies par une voiture et vecteur vitesse, extrait de Martin, 1988, p.43.
Conclusion
Notre brève enquête sur les rôles sémiotiques joués par les flèches dans des manuels scolaires de physique nous a conduits à identifier une pluralité de rôles, dont voici brièvement une synthèse :
1. un rôle de pointage, où la flèche fonctionne comme un déictique graphique ;
2. un rôle de signifiant désignant7 une force appliquée à un moment précis ;
3. un rôle de signifiant dénotant une somme des forces appliquées sur un objet à un moment précis ;
4. un rôle de signifiant dénotant un mouvement ou une trajectoire ;
5. un rôle de signifiant dénotant un vecteur, son sens et sa direction et éventuellement son intensité.
Si ce n’était pour le rôle de pointage, qui oriente l’attention et, en ce sens, ne représente rien, nous pourrions être tentés de considérer la flèche un signe ayant de multiples signifiants, un peu comme un mot disposant d’entrées distinctes dans un dictionnaire. Par exemple, livre désigne un objet plein de mots, mais aussi la moitié d’un kilogramme. Ce n’est pourtant pas si simple : l’orientation de la flèche, son sens et, dans certains usages, son tracé ou la longueur de son tracé fonctionnent comme signifiants. Cela dépend du rôle sémiotique joué par la flèche : il est inutile de considérer la longueur du tracé d’une flèche dont le rôle est de pointer une partie spécifique d’un schéma, alors que la longueur d’une flèche dénotant un vecteur peut effectivement s’interpréter comme une grandeur non quantifiable qui dénote l’intensité du vecteur en question.
De plus, certains rôles ne sont pas exclusifs mais, bien au contraire, se complètent plutôt. Par exemple, la désignation d’une force appliquée sur un objet à un instant précis peut, en même temps, dénoter le vecteur mathématique qui permet de calculer l’intensité de la force en question. Nous avons décidé de les distinguer, car un lecteur peut interpréter correctement l’un des rôles mais pas l’autre. D’une manière plus générale, les rôles 2, 3 et 4 participent à la modélisation du phénomène étudié, quoique de différentes manières. L’interprétation de la flèche dans ces rôles sémiotiques là dépend, dès lors, de ce que l’interprétant parvient à comprendre du modèle qui lui est présenté ou, s’il est l’auteur du schéma, de sa propre modélisation (au sens d’un processus cognitif). Quoi qu’il en soit, on peut dire qu’il y a là un espace pour des interprétations divergentes du moment que les rôles sémiotiques ne sont pas différenciés par les acteurs.
Concernant les résultats de nos analyses de la cohérence interne et externe des usages de l’objet sémiotique flèche, les nombreuses difficultés que nous avons pu mettre en évidence à partir de quelques exemples seulement nous donnent l’impression générale d’un langage sauvage, au sens d’un mode sémiotique qui permet effectivement la communication — et en particulier là où elle est difficile verbalement ou mathématiquement — mais qui n’est pas éduqué. Si les schémas et esquisses, dont l’objet flèche n’est qu’un élément, font partie intégrante de l’enseignement des sciences, c’est un langage graphique et visuel qui ne suit que peu de conventions, et ne respecte visiblement pas des règles comme c’est le cas pour d’autres langages (le dessin technique, l’algèbre, la syntaxe française, etc.). Pourtant, les moyens de prendre des précautions existent, et nous les avons soulignés au fil des analyses : flèches pleines ou traitillées, couleurs, et légendes sont autant de moyens à disposition pour fournir des indices au lecteur et le soutenir dans ses efforts d’interprétation.
Références
Benson, H. (1999). Physique 1. Paris, Bruxelles : De Boeck Université.
Faucher, R. (1961). Physique. Classe de seconde, sections C et M. Paris : Éditions Hatier.
Grize, J.-B., (1996). Logique naturelle & communications. Paris : PUF.
Kohler, A. (2014) Cause and Catalyst: A Differentiation. In: Cabell, K.R., and Valsiner, J. (Ed.), The Catalyzing Mind, Springer New York.
Koyré, A., (1968). Etudes newtoniennes. Paris : Gallimard.
Martin, G. (Dir.) (1988). Physique 1re S/E. Collection G. Martin. Paris : Éditions Bordas.
Pierrard, M.-A. (Dir.) (2009). Enseigner les sciences expérimentales à l’école élémentaire. Physique et technologie. Paris : Éditions Bordas.
Viennot, L. (1979). Le raisonnement spontané en dynamique élémentaire. Paris : Hermann.
Viennot, L. (1996). Raisonner en physique, la part du sens commun. Bruxelles : De Boeck.
http://www.uqac.ca/algvecto/AlgVectof4htsu57.xml
http://sgbd.ac-poitiers.fr/bde/exos/98LGB014/98LGB014.htm
[1] Il convient de préciser que tous les exemples fournis dans ce document sont présentés à titre d’illustration de propos théoriques émis par les auteurs à des fins de recherche et d’analyse. Ces exemples ne constituent donc ni une critique des ouvrages cités, ni une évaluation prenant parti dans la compétition commerciale des manuels. Il convient d’insister sur le fait que les illustrations tirées des manuels cités ont été sélectionnées à dessein, et ne sont dès lors pas représentatives de la qualité des manuels dans leur ensemble.
[2] Ces situations sont caractérisées par la quasi-absence d’accélération, et donc la quasi-disparition de l’inertie; c’est par exemple le cas du mouvement d’une bille dans la mélasse.
[3] Imaginons un wagonnet de deux tonnes qu’on tire vers l’arrière pour tenter de l’arrêter: traction et frottement auront alors le même sens, opposé au mouvement.
[4] extrait de http://www.uqac.ca/algvecto/AlgVectof4htsu57.xml
[5] À une telle question, l’enseignant pourrait répondre par une autre question caractérisée par le même non-sens: « Qu’est-ce qui est le plus long: 2 mètres ou 3 mois? »
[6] extrait de http://sgbd.ac-poitiers.fr/bde/exos/98LGB014/98LGB014.htm
[7] Nous faisons notamment usage de la sémiotique proposée par Grize (1996) pour qualifier ces rôles.